Per gran parte della storia le comete sono state considerate semplici eventi atmosferici. Nell’astronomia occidentale il primo importante passo avanti verso la comprensione della fisica delle comete fu fatto dal medico veronese Girolamo Fracastoro (1478-1553). Osservando tre comete, una nel 1531 e due nel 1532, Fracastoro si accorse che la coda era sempre in direzione opposta al Sole. L’importante scoperta, in netto contrasto con la fisica aristotelica che non prevedeva dovesse esserci una correlazione fra il Sole e la direzione della coda, fu annunciata in un’opera pubblicata nel 1538. La stessa scoperta fu fatta indipendentemente dall’astronomo tedesco Pietro Apiano (1495-1552) con la cometa del 1532.
Oggi sappiamo che le code delle comete sono almeno di due tipi: la coda di polveri e la coda di ioni. La coda di polveri è composta dai frammenti solidi che si staccano dal nucleo in seguito alla sublimazione dei materiali volatili superficiali, vanno a formare la chioma e vengono sospinti in direzione opposta al Sole dalla pressione della radiazione solare. Mentre si allontanano dal nucleo i granelli di polvere mantengono inalterato il loro momento angolare perché sia la forza di gravità, sia la pressione della radiazione agiscono in senso radiale. Come conseguenza più si allontanano dal Sole, più la loro velocità diminuisce, quindi il nucleo cometario tende a lasciarseli indietro e la forma della coda di polveri assume una forma incurvata. La coda di ioni viene generata in seguito all’interazione degli ioni presenti nella chioma della cometa con il vento solare, il flusso di elettroni, protoni e nuclei di elio che il Sole rilascia continuamente nello spazio. In questo caso la direzione della coda di ioni è data dalla composizione della velocità del nucleo con quella del vento solare e quindi non sarà in direzione esattamente opposta al Sole.
In prima approssimazione, possiamo considerare la coda di ioni o polvere opposta al Sole e vedere come se ne può stimare l’effettiva lunghezza nello spazio a partire dalla misura dell’angolo sotteso nelle immagini. Come esempio prendiamo la cometa C/2002 E3 (ZTF), ben visibile in questa seconda metà del mese di agosto 2022 nella costellazione di Ercole.

Si tratta di una cometa che si muove su un’orbita nominale leggermente iperbolica, il che ne indica l’origine nella nube di Oort. Questa cometa dovrebbe diventare visibile a occhio nudo fra la fine di gennaio e l’inizio di febbraio 2023, quindi merita attenzione durante l’avvicinamento al perielio.
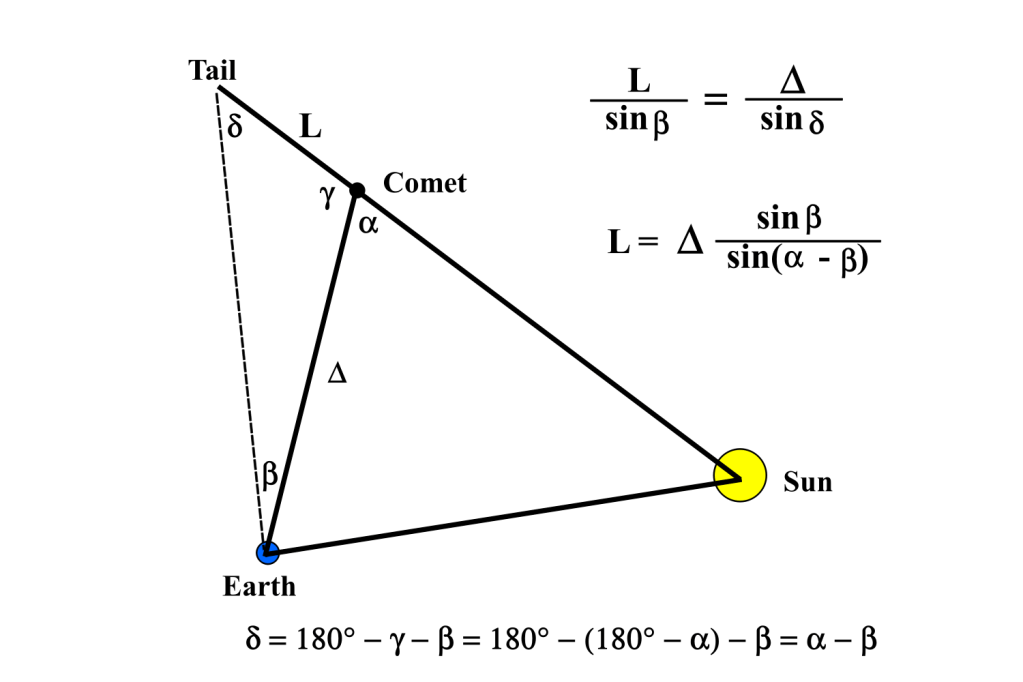
In immagini riprese la sera del 16 agosto 2022 questa cometa mostrava una coda di polveri della lunghezza di circa 4 primi d’arco ossia 0,067°. La misura della lunghezza è stata fatta con il software Astrometrica, che ha la possibilità di mostrare la distanza fra due punti arbitrari dell’immagine. A quanto equivale nello spazio l’angolo sotteso dalla coda? Supponiamo che la coda sia ortogonale alla linea di vista, non è vero ma è un primo passo verso la soluzione. Dalle effemeridi sappiamo che la cometa era a circa 2,135 au = 319,4 milioni di km dalla Terra, quindi se la coda sottendeva 0,067° doveva avere almeno una lunghezza L = 319,4 * (0,067°/57,29°) = 370.000 km. In questo calcolo approssimato abbiamo sfruttato il fatto che, se l’angolo sotteso è piccolo, la tangente dell’angolo è praticamente uguale all’angolo stesso espresso in radianti (57,29° è la misura in gradi di un radiante). Questo è solo un limite inferiore, in realtà la geometria con cui abbiamo a che fare è quella della Fig. 2. Qui siamo nel piano identificato da tre corpi: il nucleo cometario, la Terra e il Sole. Delta è la distanza Terra-cometa, mentre alfa è l’angolo di fase ossia l’angolo Terra-cometa-Sole. Infine beta è l’angolo sotteso dalla coda osservata dalla Terra. Siamo nel caso di una geometria piana, quindi si può applicare il teorema dei Seni al triangolo Tail-Comet-Earth per ricavare L, la lunghezza della coda. La formula per L che si trova è riportata direttamente nella Fig. 2. Applicandola al nostro caso tenendo conto che, dalle effemeridi, alfa = 24,2° si trova L = 913.000 km ossia arrotondando, circa 1 milione di km. In conclusione la lunghezza reale della coda della cometa C/2022 E3 nello spazio è quasi 3 volte quella che si otterrebbe dalla semplice ipotesi di ortogonalità alla linea di vista. Ricordiamolo la prossima volta che ci sarà da stimare la lunghezza della coda di una cometa.
L’ha ripubblicato su ARIA NUOVA ITALIA.
"Mi piace""Mi piace"