Nell’articolo precedente sulla spettroscopia avevamo illustrato il setup hardware e software per ottenere spettri delle stelle più luminose in cielo utilizzando un semplice reticolo di diffrazione posto davanti al teleobiettivo di una DSLR. Avevamo visto come calibrare lo spettro di Sirio in lunghezza d’onda usando il software RSpec ed eravamo giunti alla conclusione che la forma dello spettro continuo era alterata sia dalla curva di risposta strumentale sia dallo scattering di Rayleigh dovuto alle molecole e alla polvere atmosferica. In questa seconda parte vogliamo imparare a ottenere la curva di risposta strumentale e come compensare lo scattering Rayleigh, così da riportare lo spettro osservato alla sua forma reale. Non useremo Sirio, ma la stella Phi Persei, molto più interessante dal punto di vista astrofisico. Prima, però, vediamo la relazione matematica che permette di passare dallo spettro osservato a quello effettivo della stella.

Curva di risposta strumentale: la teoria

Se chiamiamo S(λ, x) lo spettro osservato, che dipende dalla lunghezza d’onda e dall’airmass x, S*(λ) lo spettro intrinseco o effettivo della stella, C(λ) la curva di risposta strumentale (che dipende dal telescopio e dal rivelatore usati), e K_atm(λ) l’estinzione atmosferica in funzione della lunghezza d’onda misurata in mag/airmass, allora vale la relazione (Button C. et al., 2013):

S(λ, x) = S*(λ)⋅C(λ)⋅10^{-0,4⋅K_atm(λ)⋅x} (1)

L’intensità S(λ, x) è una funzione della lunghezza d’onda (ad airmass fissata), ed è lo spettro osservato della stella, quello che si ottiene direttamente con RSpec, quindi è una quantità nota. S*(λ) è lo spettro, dello stesso tipo di quello osservato, proveniente dalla libreria di RSpec, quindi è noto anche questo. La funzione C(λ) è quella che vogliamo ottenere, a patto di conoscere K_atm(λ), ossia l’estinzione atmosferica. Quest’ultima è composta da due termini additivi, dovuti allo scattering Rayleigh sia delle molecole atmosferiche sia della polvere che hanno due dipendenze diverse dalla lunghezza d’onda della radiazione:

K_atm(λ) ≈ R⋅(λ/λ₀)^-4+A⋅(λ/λ₀)^-1,3 (2)

Il primo termine è dovuto allo scattering molecolare; il secondo, alle polveri, entrambi con λ0 = 5500 Å. Ci sarebbero anche ulteriori termini dovuti all’ozono e alle bande molecolari dell’acqua, ma possiamo trascurarli rispetto ai primi due contributi che sono dominanti. Il valore delle costanti R e A dipende dallo stato effettivo dell’atmosfera, tipicamente vale R ≈ 0,13 mag/airmass e A ≈ 0,05 mag/airmass. Assumeremo questi valori, consapevoli che la correzione non sarà perfetta; pertanto, sarà d’obbligo ottenere la risposta strumentale con stelle ben alte sull’orizzonte, così da minimizzare l’effetto dello scattering Rayleigh. Per il valore x dell’airmass vale la relazione approssimata x ≈ 1/cos(z), dove z è la distanza zenitale della stella. Per z = 0 (stella allo zenit), l’airmass è 1, mentre per z = 30° è 1,15 e così via. Questa relazione vale esattamente per un’atmosfera a facce piane e parallele. Considerato che la Terra è sferica, va bene per stelle con distanza zenitale fino a circa 60°. Per distanze zenitali superiori, è necessario usare formule più complesse che tengano conto della sfericità della Terra, ma ciò esula dal nostro caso, poiché vogliamo osservare stelle non troppo distanti dallo zenit, così da minimizzare l’influenza dello scattering Rayleigh. Nota quindi l’estinzione atmosferica in funzione della lunghezza d’onda, la funzione di risposta strumentale è data da:

C(λ)=[S(λ, x)/S*(λ)]⋅10^{+0,4⋅K_atm(λ)⋅x} (3)

In breve: bisogna riprendere lo spettro di una stella ad almeno 30° di altezza sull’orizzonte, calibrarlo in lunghezza d’onda, come abbiamo visto nella prima parte, normalizzarlo a 1 a 5500 Å e dividerlo per l’analogo spettro della libreria di RSpec. Giunti a questo punto, basta moltiplicare il risultato per il coefficiente di correzione atmosferica per ottenere la curva di risposta strumentale. Una volta nota la curva C(λ), la potremo applicare a qualsiasi spettro osservato per ottenere il vero spettro della sorgente:

S*(λ)=[S(λ, x)/C(λ)]⋅10^{+0,4⋅K_atm(λ)⋅x} (4)

Per mitigare gli effetti dello scattering atmosferico, si possono determinare diversi valori di C(λ) utilizzando stelle diverse, per poi ottenere una curva media della risposta strumentale. Se le cose sono andate per il verso giusto, da una curva all’altra non dovrebbero esserci differenze rilevanti.

Lo spettro di Phi Persei

Phi Persei (o φ Persei) è un sistema stellare di magnitudine apparente +4, a circa 720 anni luce da noi. Si tratta di una binaria spettroscopica composta da una stella primaria di sequenza principale blu di classe spettrale B1.5V, con una massa 10 volte quella del Sole, e da una stella subnana di 1,14 M_☉ di tipo spettrale O. Quest’ultima è molto calda ed emette quasi tutta la sua energia nell’ultravioletto, quindi lo spettro nel visibile di Phi Persei è praticamente dovuto alla sola primaria. Le due stelle percorrono un’orbita di 217 giorni attorno al centro di massa comune e sono separate da circa 200 R_☉ (raggi solari). La primaria ruota molto rapidamente attorno al proprio asse, tanto che la forma della stella non è sferica, ma schiacciata, e rilascia gas nello spazio dalle regioni equatoriali; per questo motivo è circondata da un disco circumstellare, responsabile della presenza di righe in emissione nello spettro. In effetti, se vogliamo essere precisi, la primaria è di tipo spettrale B1.5Ve, dove la “e” alla fine della sigla dello spettro sta per presenza di “righe in emissione”. Le righe in emissione sono dovute al disco di gas in espansione che circonda la stella, che assorbe la radiazione e la riemette nello spazio. Più in generale, la primaria del sistema binario di Phi Persei appartiene alla classe delle stelle Be, un insieme eterogeno di stelle di tipo spettrale B con le righe di Balmer in emissione. L’esempio più noto di stella Be è la stella gamma di Cassiopea (γ Cas oppure γ Cassiopeiae), ben visibile a occhio nudo nell’omonima costellazione.

Questa stella è stata ripresa con la strumentazione descritta nella prima parte di questo articolo il 9 dicembre 2025 con tempi di posa di 15 s a 1600 ISO. Nel complesso, sono state riprese 30 immagini, mediate per ottenere un miglior rapporto segnale-rumore. Dopo aver calibrato in lunghezza d’onda ed eliminato le parti non necessarie con il procedimento già visto con RSpec, lo spettro raw si presenta come mostrato in Fig. 1.

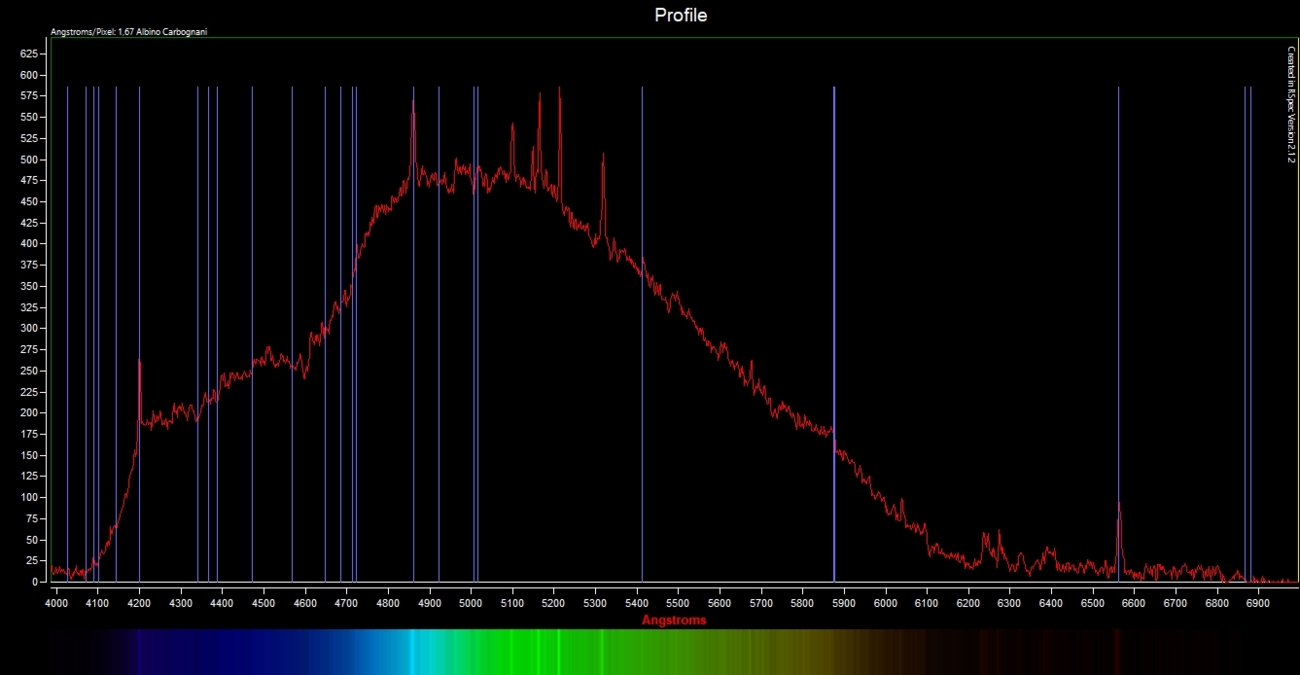
Nello spettro raw di Fig. 1 si osservano diverse righe in emissione, tra cui l’H-alpha e l’H-beta della serie di Balmer, mentre l’H-delta è in assorbimento. Notevole anche una riga in emissione a 4200 Å, dovuta all’HeII o all’NII, rispettivamente all’elio e all’azoto ionizzati una volta.

L’estrazione smooth dello spettro continuo

Ora che abbiamo lo spettro raw di Phi Persei, ossia S(λ, x), prima di dividerlo per S*(λ) per poter applicare l’Eq. (3), dobbiamo togliere le righe di emissione più pronunciate e “lisciare” (ossia rendere smooth) la curva in modo da estrarre la sola parte dello spettro continuo. La stessa cosa andrà fatta per lo spettro della libreria di riferimento di RSpec avente lo stesso tipo spettrale della stella osservata. Questa operazione è necessaria, altrimenti la presenza delle righe, in assorbimento o in emissione che siano, altererebbe la curva di risposta strumentale C(λ), quindi è bene prendere stelle di tipo B in cui le righe in assorbimento non sono così profonde come in quelle di tipo A, F o G. Per eliminare le righe dello spetto basta attivare le linee di misura fleggando “Show Measure lines“, posizionarle con il mouse in modo che contengano, di stretta misura, la riga da cancellare e cliccare sul pulsante “Reference -> Edit Points”. Si aprirà così la finestra “Edit” e, cliccando su “Delete”, la riga sparirà dallo spettro: al suo posto comparirà una semplice interpolazione lineare. Si deve ripetere l’operazione per tutte le righe presenti. Tolte le righe più importanti, sempre nella finestra “Edit”, si potrà agire sul cursore del riquadro “Spline Smoothing“, per lisciare definitivamente la parte continua dello spettro. L’operazione di spline è una tecnica di regressione non parametrica che genera una curva liscia a partire da dati rumorosi e va applicata con cautela, per lisciare lo spettro continuo, mantenendo la corretta pendenza media in ogni punto della curva. Per questo bisognerà “sperimentare” con i comandi “Coarse Adjust” e “Fine Adjust” fino a ottenere la curva interpolante corretta che apparirà di colore blu e sarà indicata come “reference”. A questo punto si può chiudere la finestra “Edit” premendo sul pulsante “Close”. Prima di salvare lo spettro continuo smooth va prima normalizzato a 1 a 5500 A. Per questo si deve usare il pulsante “Reference -> Math”, così da aprire la finestra “Math”, si seleziona “Reference” in “Parameter 1” (in questo modo si agisce solo sulla curva blu), il simbolo della divisione “/” in “Operation” e si mette il valore dello spettro lisciato a 5500 A in “Parameter 2”. L’intensità dello spettro della curva blu a 5500 Å si legge scorrendo la curva con il mouse. Fatto questo, basta premere il pulsante “Calculate” nella finestra “Math” per ottenere la preview della curva dello spettro normalizzata a 1 che si può visualizzare nella finestra principale cliccando su “Move to Main Profile”. Ora possiamo chiudere la finestra Math e salvare la curva smooth dello spettro continuo premendo il pulsante con l’icona del dischetto da 3,4″. In questo modo nella cartella di lavoro verrà salvato un file di testo con estensione .dat che riporta due colonne: la prima è la lunghezza d’onda in Å, mentre la seconda è l’intensità dello spettro. Questo file è la nostra funzione S(λ, x). La stessa operazione di smooth andrà eseguita sullo spettro dello stesso tipo di quello osservato, caricato dalla libreria di RSpec. Qua la normalizzazione a 1 a 5500 Å non è necessaria perché lo è già di partenza. Prima di procedere, andranno cancellati i punti al di fuori dell’intervallo spettrale osservato. Se lo spettro smooth osservato va da 4000 a 7000 Å, anche quello smooth della libreria andrà limitato allo stesso intervallo, usando le due linee di misura e la finestra “Edit” vista prima. Lo spettro della libreria, croppato e reso smooth, andrà salvato con lo stesso nome originale, a cui si aggiunge “_smooth” per distinguerlo da quello originale: questa è la funzione S*(λ). Così facendo, non si modifica la libreria nativa degli spettri di RSpec.

Curva di risposta strumentale: la pratica

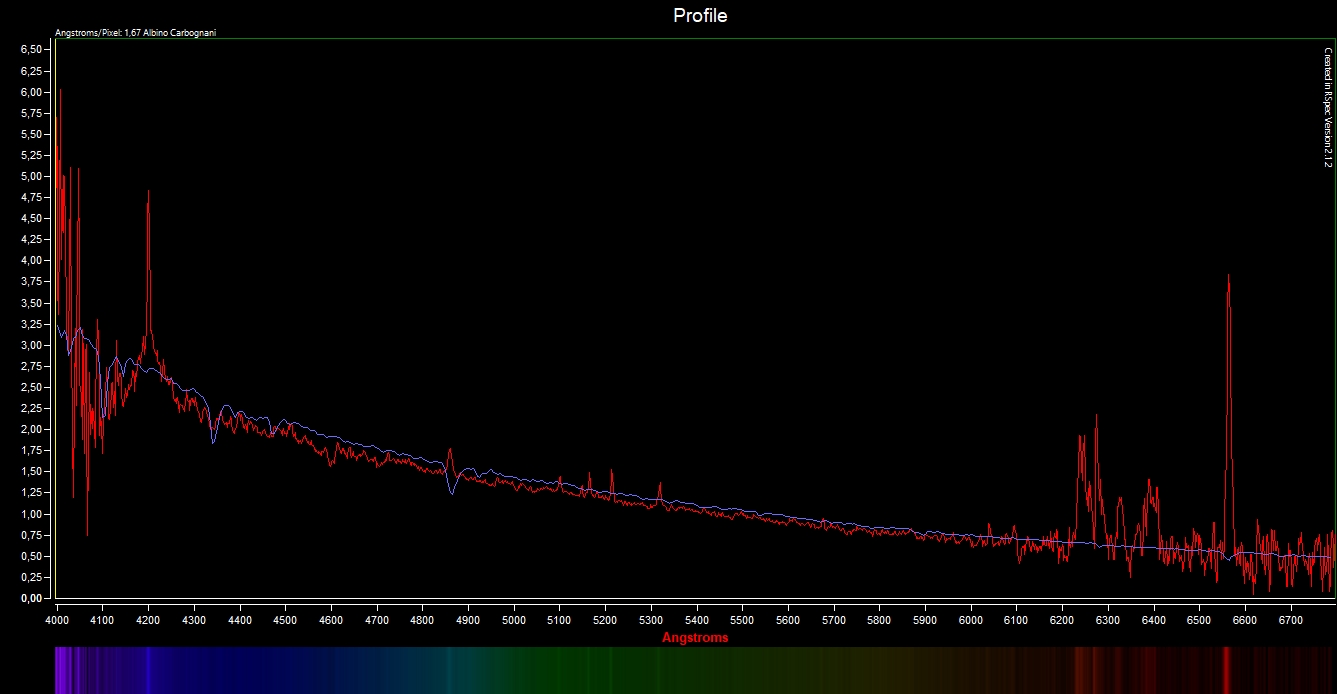
Ora che abbiamo le curve smooth sia dello spettro osservato sia di quello della libreria, possiamo dividere le due funzioni tra loro, così da ottenere il fattore S(λ, x)/S*(λ) dell’Eq. (3). Per questo, usando il menù “Open profile” va prima caricato lo spettro smooth osservato e poi, con il menù “Reference -> Open Reference Series“, va caricato lo spettro smooth di riferimento: il primo apparirà di colore rosso, il secondo di colore blu. Adesso, come prima, apriamo la finestra “Math”, ma ora, in “Parameter 1”, bisogna selezionare “Main Profile“, mentre in “Parameter 2” va selezionato “Reference“. L’operazione di divisione resta sempre la stessa. Cliccando sul pulsante “Calculate“, il risultato della divisione tra le due curve per ogni valore di lunghezza d’onda è visualizzato nella finestra Math, come mostrato in Fig. 2.

Il risultato della divisione fra le due curve va trasferito nella finestra principale cliccando su “Move to Main Profile” e poi salvato in un file .dat, come già visto. Ora resta da moltiplicare per la parte esponenziale, così da ottenere la funzione C(λ) secondo l’Eq. (3). Sfortunatamente, RSpec non dispone di un tool per la correzione dello scattering Rayleigh, quindi bisogna scrivere uno script in Python o Matlab che esegua l’operazione per noi. Nel nostro caso abbiamo utilizzato Matlab e il risultato è mostrato in Fig. 3. La curva di risposta strumentale raw è quella rossa ed è data da S(λ, x)/S*(λ). Quella corretta per lo scattering Rayleigh è quella blu ed è la C(λ) data dall’Eq. (3). Questa curva potrà essere utilizzata nell’Eq. (4) per correggere tutti i tipi di spettri osservati, senza doverla ottenere tutte le volte, purché si usi lo stesso strumento, mentre la parte relativa allo scattering Rayleigh sarà diversa, in quanto dipende almeno dalla distanza zenitale del target. Per verificare che tutto sia andato bene si può confrontare lo spettro osservato, corretto per la risposta strumentale e lo scattering Rayleigh, con quello della libreria e a questo punto i due dovrebbero essere sovrapponibili, vedi Fig. 4. Volendo, si possono osservare alcune stelle in prossimità dello zenit in modo da verificare che la curva di risposta strumentale C(λ) sia sempre la stessa. Piccole differenze potranno essere dovute a una correzione non perfetta per lo scattering di Rayleigh, anche se l’osservazione in prossimità dello zenit minimizza l’effetto di tale correzione. RSpec consente di applicare automaticamente la correzione della risposta strumentale a tutti gli spettri ripresi tramite il menù “Adjust for Instrumental Response“, che si apre cliccando sull’icona con la ruota colorata.

La misura della temperatura delle stelle

Giunti a questo punto del nostro “laboratorio”, abbiamo tutti gli strumenti per misurare la temperatura superficiale di una stella; prima, però, è necessario un cenno al corpo nero. In fisica un corpo nero è un oggetto ideale che assorbe tutta la radiazione incidente sulla sua superficie (da qui il nome) e che emette radiazione elettromagnetica secondo una legge che dipende solo dalla temperatura, non dal materiale di cui è composto. Lo spettro di emissione di un corpo nero è quindi uno spettro continuo, con una forma definita dalla legge di Planck, che ha la forma di una campana asimmetrica: l’emissione tende a zero per le lunghezze d’onda piccole e grandi, mentre il massimo dell’emissione si ha a una lunghezza d’onda λmax che dipende dalla temperatura T secondo la relazione λmaxT=costante (legge di Wien). In base alla legge di Wien, un corpo nero, all’aumentare di T, il massimo dell’emissione si sposta dal rosso al blu dello spettro. Un buon esempio di radiazione con un profilo di corpo nero è quella emessa dalla bocca di un forno mantenuto a temperatura costante: la radiazione emessa e assorbita innumerevoli volte dalle pareti del forno è in equilibrio termico con la materia del forno stesso e lo spettro è proprio quello previsto da Planck (che, per inciso, fu uno dei fattori di crisi della fisica classica che portarono alla meccanica quantistica). La luce che vediamo da una stella nasce nella fotosfera, uno strato di gas così denso e otticamente spesso che la radiazione subisce molte interazioni con la materia prima di uscire. Questo tende a “termalizzare” la radiazione, facendo sì che l’emissione complessiva del continuo stellare assomigli molto a quella di un corpo nero. Lo spettro di una stella è più complesso dell’andamento previsto da Planck, perché ci sono le righe di emissione e assorbimento. Tolte queste, il continuo è, con una buona approssimazione, quello di un corpo nero. Questo fatto può essere sfruttato per ottenere una stima ragionevole della temperatura fotosferica della stella, considerando l’intero continuo osservato fra 4000 e 7000 Å.

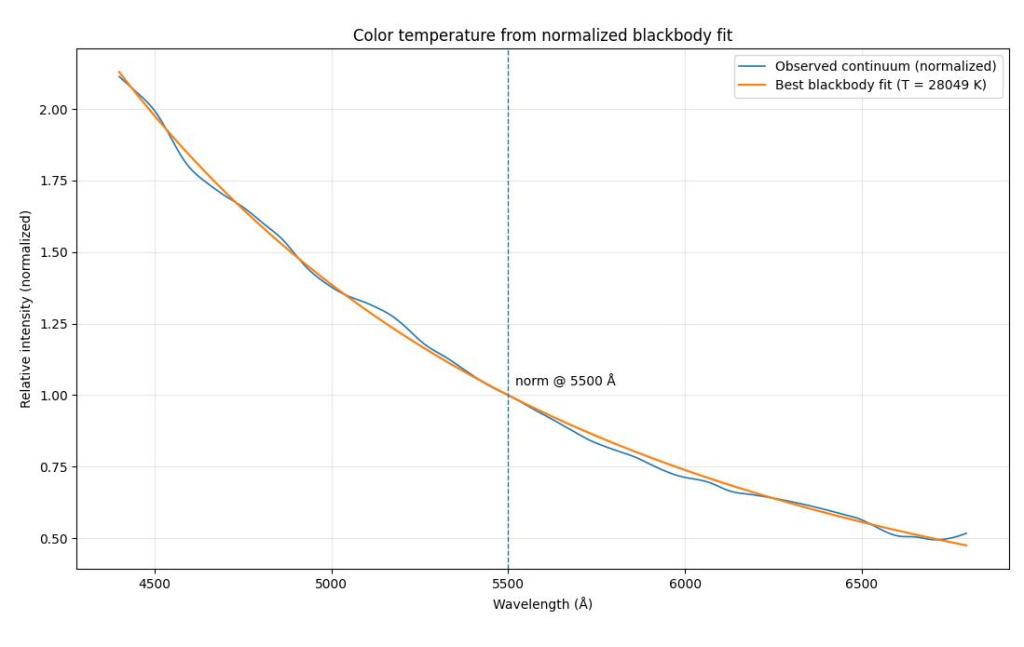
Una volta corretto lo spettro osservato per la risposta strumentale e lo scattering Rayleigh, si possono eliminare le righe di assorbimento e di emissione in modo da isolare solo lo spettro continuo della stella e, come abbiamo già visto prima, farne la versione “smooth” con RSpec. Con lo spettro continuo della stella “lisciato”, possiamo fittare ai minimi quadrati la migliore curva di corpo nero normalizzata a 1 a 5500 Å che riproduca lo spettro osservato e ottenere così una stima della temperatura della stella. Per ottenere questo risultato è necessario scrivere un software che faccia il lavoro (ad esempio si può usare il linguaggio Python). In alternativa, si può usare la “Planck Library” di RSpec, che riporta diverse curve di Planck da 1600 a 30.000 K, che possono essere confrontate con il continuo osservato per ottenere una stima grossolana della temperatura. Se si applica la procedura qua delineata al caso di Phi Persei, si ottiene una temperatura di corpo nero pari a T = 28.050 K, che è sostanzialmente la temperatura corretta per la componente A di Phi Persei, vedi Fig. 5.

Lo spettro dei lampioni a LED

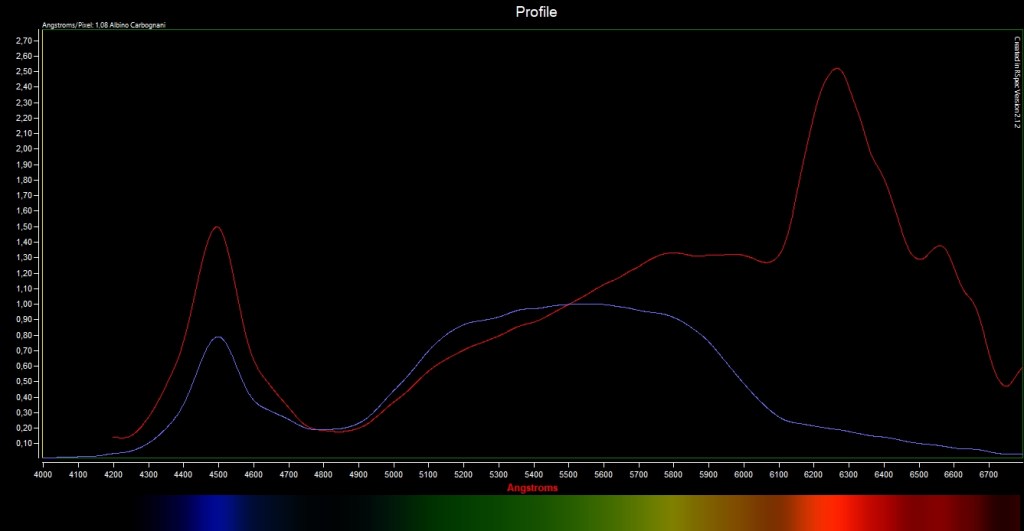
Nel nostro laboratorio di spettroscopia abbiamo ripreso lo spettro dei lampioni a LED del paesino di Loiano, che causano un grave inquinamento luminoso. Lo scopo era verificarne la temperatura di colore. Tipicamente, i LED per illuminazione pubblica presentano un picco nel giallo-rosso e uno nel blu; in base all’altezza del picco blu, la luce complessiva è più o meno bianca e determina la temperatura di colore del LED. Naturalmente, il picco nel blu è responsabile di una buona parte dell’inquinamento luminoso perché, come si vede dall’Eq. (2) dello scattering Rayleigh, alle brevi lunghezze d’onda il coefficiente di estinzione atmosferica aumenta, il che significa che la radiazione viene diffusa da tutte le parti dalle molecole e dalla polvere atmosferica. Nella ripresa dei LED con il teleobiettivo dotato di reticolo di diffrazione, l’unica accortezza è la ripresa di scorcio, in modo che il LED appaia come una sottile striscia luminosa parallela alle righe del reticolo. Naturalmente, anche qua bisogna prestare attenzione alla saturazione nel verde, che distorcerebbe lo spettro. In questo caso l’airmass è x = 0 e l’Eq. (4) si semplifica perché la parte esponenziale vale sempre 1. In sostanza, basta dividere lo spettro raw per la sola curva di risposta strumentale per ottenere il vero spettro della sorgente. Il risultato è riportato in Fig. 5. Come si vede, il picco nel blu è circa il 60% di quello nel rosso, quindi la temperatura di colore è di circa 3000 K, il valore limite che si è data la regione Emilia-Romagna nella legge per limitare l’inquinamento luminoso. Per completezza, va detto che per temperature di colore di 2700 K, l’altezza del picco nel blu è il 30% di quello nel rosso, per 4000 K i due picchi si equivalgono, mentre per un LED a 5000 K il picco nel blu è il 30% più alto di quello del rosso. Tornando al limite superiore di 3000 K, ovviamente niente impedisce di installare LED a una temperatura di colore inferiore, come 2000-2500 K, per avere un picco blu più ridotto e minimizzare lo scattering Rayleigh, ma, purtroppo, questa scelta per Loiano non è stata fatta.